Un límite, es un valor fijo al que tienden, sin alcanzarlo, los términos de una serie infinita de números.

En un límite, podemos estudiar los límites laterales, cuando el límite de una función tiende a la izquierda, en rojo (-), y cuando tiende a la derecha, en negro (+).

* NUNCA confundas una función con un límite.




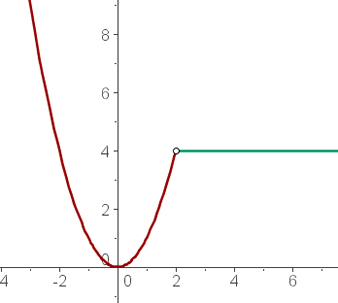
EJEMPLO DE LA IMAGEN.






En este caso, cuando x vale 2, y vale 2, en este caso no sería necesario calcular los límites laterales, ya que la función no requiere su estudio, ya que en tanto + como - dará 2.

Si los límites laterales no coinciden, no existe el límite.


Mira esta gráfica, calculemos el límite de esta función a trozos cuando x vale 2.

Lim (f) = 2 si Lim f(x) a+ = Lim f(x) a-
El límite cuando tiende a la izquierda, es dos, y a la derecha, igual, con lo cual, el límite si existe.